The process is isothermal, so the ideal gas law
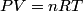 must hold (where must hold (where 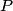 is the pressure, is the pressure, 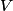 is the volume, is the volume, 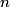 is the number of moles of the gas, is the number of moles of the gas, 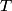 is the temperature in Kelvin, and is the temperature in Kelvin, and 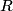 is the universal gas constant. Therefore, the work done by the gas during the expansion is is the universal gas constant. Therefore, the work done by the gas during the expansion is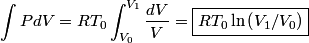 Therefore, answer (E) is correct. |